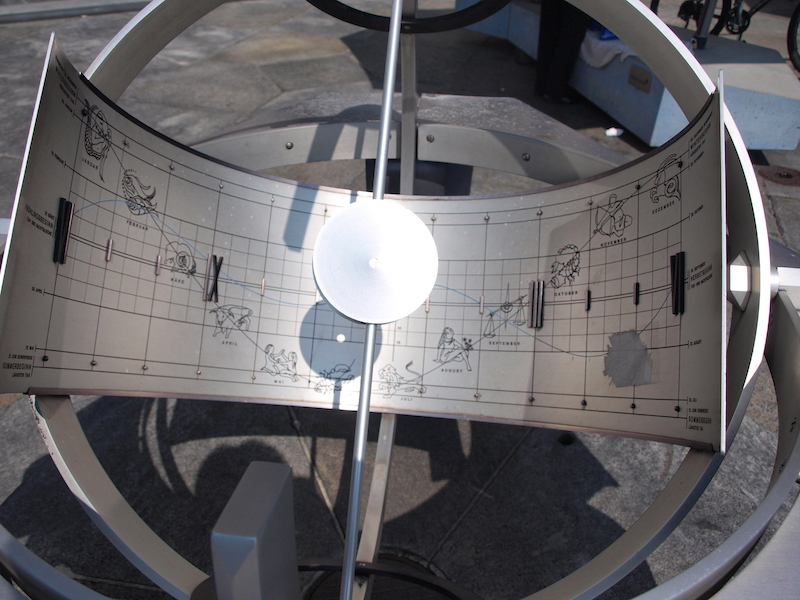
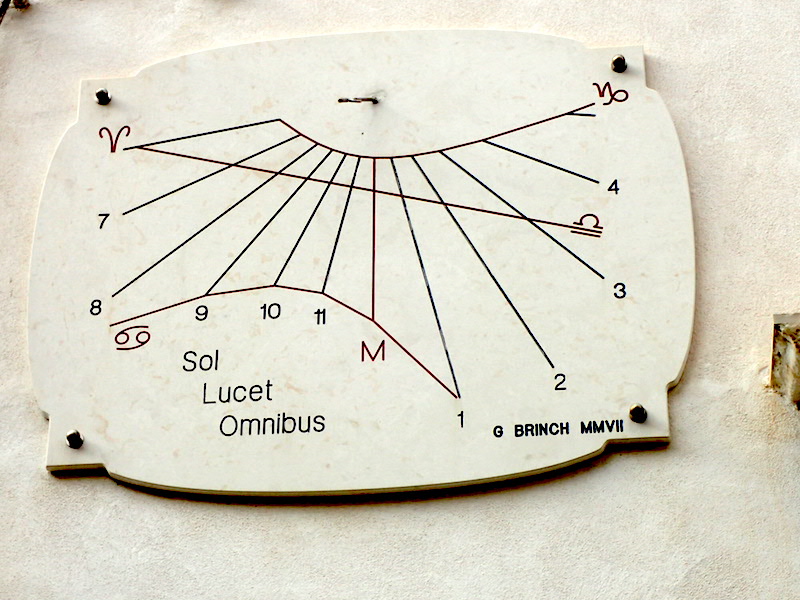
Carrer de Pescadors al Cabanyal, València, País Valencià
21 de desembre 2014, 12:41

Catí, Alt Maestrat, País Valencià
26 de novembre de 2017, 14:16

Catí, Alt Maestrat, País Valencià
26 de novembre de 2017, 14:17
Morella, Els Ports, País Valencià
30 de desembre de 2008, 14:28

Sant Carles de la Ràpita, Montsià, Catalunya.
10 d’agost de 2012, 11:56

Mosset, Conflents, Catalunya Nord.
3 de novembre de 2012, 10:01

Vilafranca de Conflent, Conflent, Catalunya Nord
2 novembre 2012, 16:11
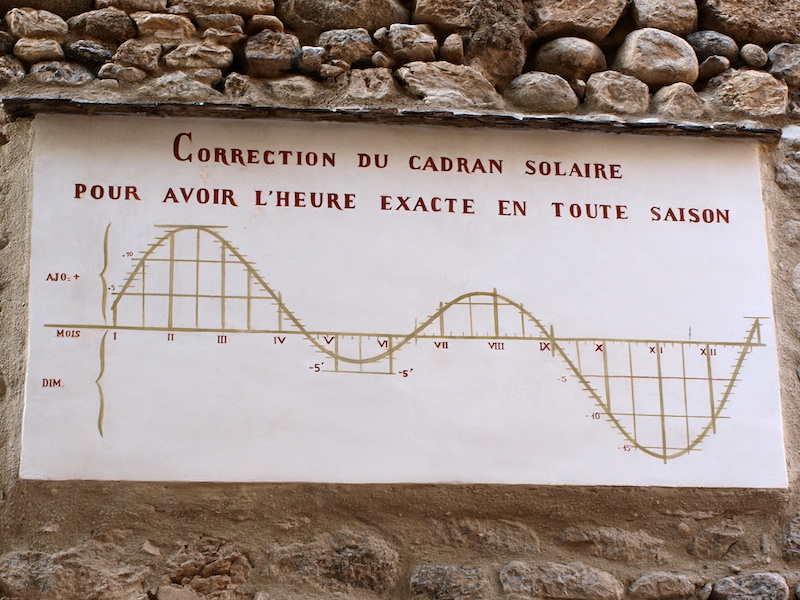
Vilafranca de Conflent, Conflent, Catalunya Nord.
2 novembre de 2012, 16:11
Gràfica de l’equació de temps en una paret per corregir els rellotges de sol.

Ermita de Nuestra Señora del Remedio, Utiel, Plana Utiel-Requena
16 de gener de 2010, 14:08

Prats de Molló, Vallespir
4 de novembre de 2007, 12:09

Prats de Molló, Vallespir
4 de novembre de 2007, 12:09