Conceptes bàsics.
Donada una circumferència c, dos punts alineats amb el centre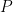 i
i  són inversos entre si quan es compleix que
són inversos entre si quan es compleix que  .
.
Per simplificar podem particularitzar a 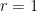 i tenim
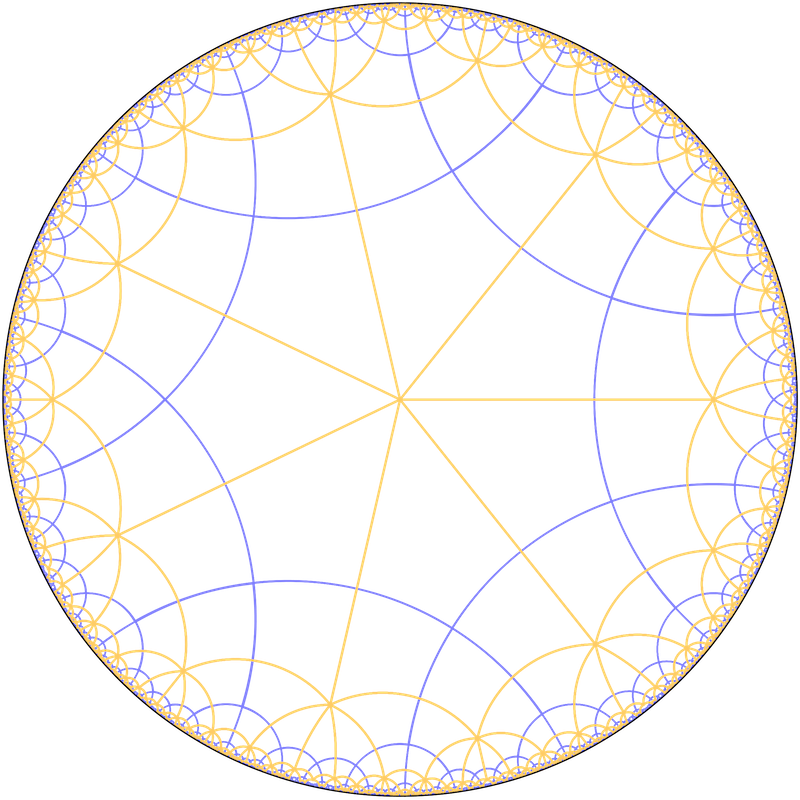
i tenim  . Estem llavors en el disc unitat que servirà de model per la geometria hiperbòlica.
. Estem llavors en el disc unitat que servirà de model per la geometria hiperbòlica.
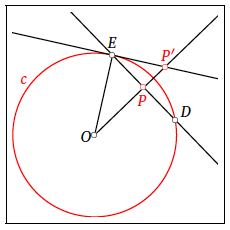
La construcció de  a partir de
a partir de 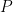 és senzilla: semirecta
és senzilla: semirecta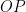 , perpendicular por
, perpendicular por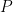 , punt intersecció
, punt intersecció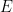 , radi
, radi , perpendicular a aquest radi ( o tangent en
, perpendicular a aquest radi ( o tangent en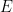 ) i
) i és la intersecció d’aquesta tangent amb la semirecta
és la intersecció d’aquesta tangent amb la semirecta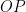 .
.
La construcció de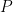 a partir de
a partir de  també és senzilla: Construïm una semicircumferència amb diàmetre
també és senzilla: Construïm una semicircumferència amb diàmetre  i trobem
i trobem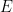 com intersecció d’aquesta semicircumferència amb la circumferència c , fent la perpendicular a
com intersecció d’aquesta semicircumferència amb la circumferència c , fent la perpendicular a  per
per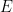 aconseguim
aconseguim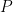 .
.
* La justificació és a partir de la semblança dels triangles  i
i  . *
. *
En una inversió tenim uns elements invariants. Un punt de la circumferència és el seu propi invers i per tant també la circumferència sencera. Les semirectes amb origen en el centre, la part interior i l’exterior són inverses entre si. També són invariants les circumferències ortogonals a la circumferència donada.
Circumferències ortogonals
La circumferència que passa per dos punts inversos respecte d’una circumferència és invariant (inversa de si mateixa). I I les duess circumferències són ortogonals (es tallen amb un angle angle recte).
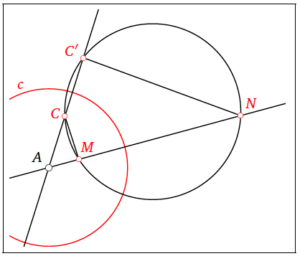
Qualsevol circumferència que passe per dos punts 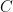 i
i  inversos respecte de c és inversa de si mateixa. Es pot veure que si tracem una recta que passe pel centre de c, els dos punts
inversos respecte de c és inversa de si mateixa. Es pot veure que si tracem una recta que passe pel centre de c, els dos punts  i
i 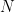 en què interseca amb la circumferència són inversos entre si.
en què interseca amb la circumferència són inversos entre si.
* La justificació es basa en la semblança dels triangles  i
i  . *
. *
Aquesta propietat ens serveix per a justificar que hi ha una circumferència que passa per dues parelles de punts inversos 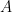 ,
,  i
i 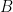 ,
,  . De totes les circumferències que passen per
. De totes les circumferències que passen per 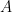 i
i  escollirem la que passe per
escollirem la que passe per 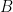 i obligatòriament passarà per
i obligatòriament passarà per  .
.
Donada una circumferència c i dos punts inversos 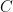 i
i  respecte d’aquesta circumferència es pot veure que si tracem qualsevol circumferència que passe
respecte d’aquesta circumferència es pot veure que si tracem qualsevol circumferència que passe 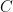 i
i  és ortogonal a la circumferència.
és ortogonal a la circumferència.
* Podem construir una justificació provant que els radis  i
i  són perpendiculars.*
són perpendiculars.*
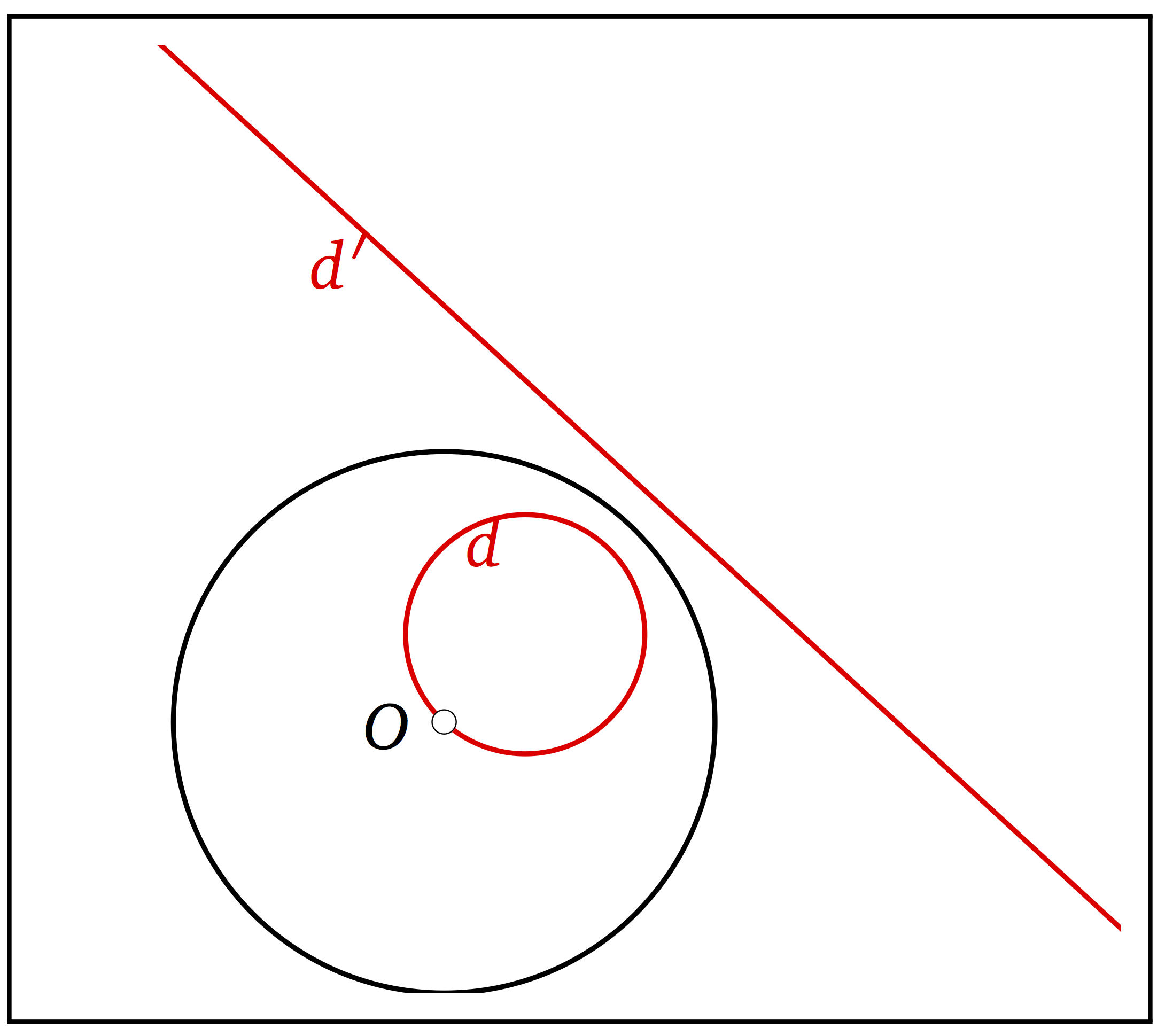
Inversa d’una recta secant a la circumferència
Són inverses entre si una recta secant respecte de la circumferència donada i una circumferència també secant que passa pel centre i pels dos punts d’intersecció de la recta tangent.
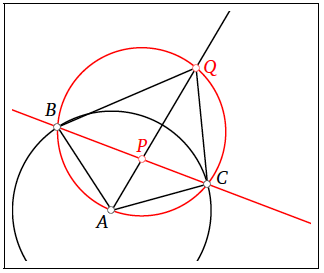
Cada punt 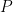 de la recta és invers d’un punt
de la recta és invers d’un punt 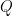 de la circumferència i viceversa. En particular el punt
de la circumferència i viceversa. En particular el punt 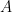 centre de la circumferència és l’invers dels punts en l’infinit de la recta.
centre de la circumferència és l’invers dels punts en l’infinit de la recta.
* Justificació mitjançant la semblança dels triangles $latexABP$ i $latexBPQ$ *
Açò ens dóna un mètode per obtenir l’invers d’un punt 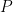 interior traçant una recta que talla en dos punts a la circumferència i dibuixant la circumferència que passa per eixos dos punts i el centre
interior traçant una recta que talla en dos punts a la circumferència i dibuixant la circumferència que passa per eixos dos punts i el centre 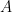 de la circumferència obtindrem l’invers
de la circumferència obtindrem l’invers 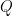 en la intersecció de la semirecta per
en la intersecció de la semirecta per 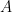 i
i 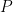 .
.
Un mètode particular per trobar l’invers  d’un punt
d’un punt 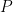 interior serà traçant una perpendicular en
interior serà traçant una perpendicular en 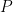 a la semirecta per
a la semirecta per 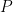 amb origen el centre i dibuixant la circumferència pels punts d’intersecció i el centre.
amb origen el centre i dibuixant la circumferència pels punts d’intersecció i el centre.
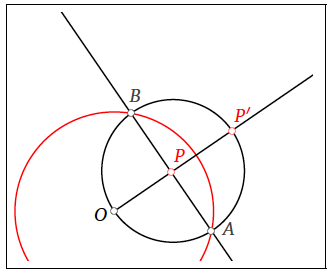
I que també ens serveix per a trobar l’invers si el un punt és exterior construint la circumferència per O centrada en el punt mitjà de  i
i  , unint els punts d’intersecció obtindríem la recta secant i el punt invers seria la intersecció d’aquesta amb la semirecta.
, unint els punts d’intersecció obtindríem la recta secant i el punt invers seria la intersecció d’aquesta amb la semirecta.
També podem usar aquesta propietat per a obtenir simultàniament els inversos de dos punts interiors traçant la recta secant que passa per ells i obtenint la circumferència que passa pels punts d’intersecció i el centre.
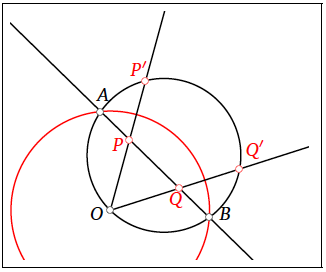
Ara podríem construir la circumferència que passa per tres dels quatre punts 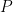 ,
,  ,
, 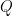 i
i 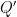 i obtindríem una circumferència que passa pel quart punt i és ortogonal a la circumferència fixada.
i obtindríem una circumferència que passa pel quart punt i és ortogonal a la circumferència fixada.
Açò ens permet obtenir fàcilment el segment hiperbòlic que uneix dos punts en la geometria hiperbòlica del disc de Poincaré.
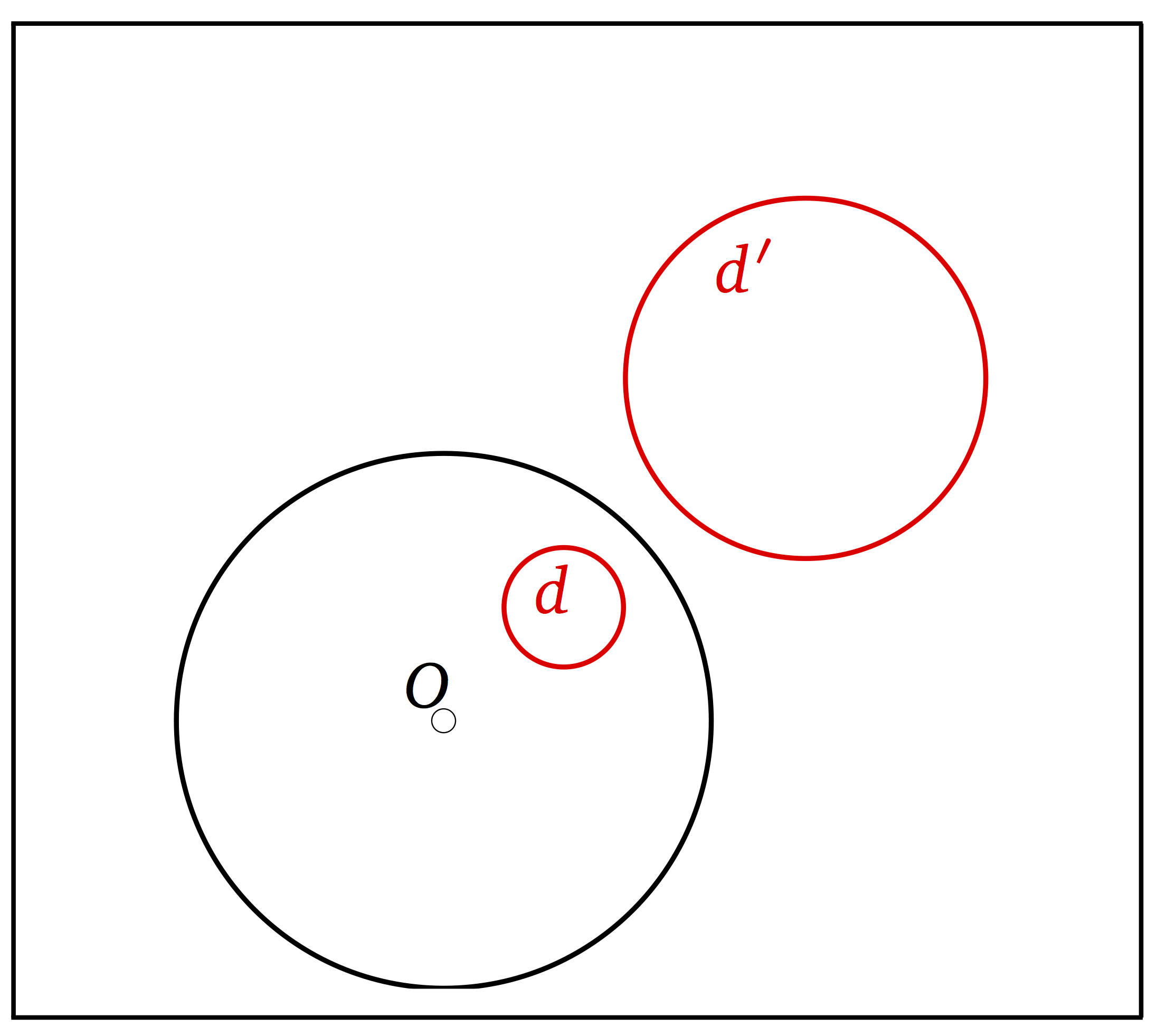
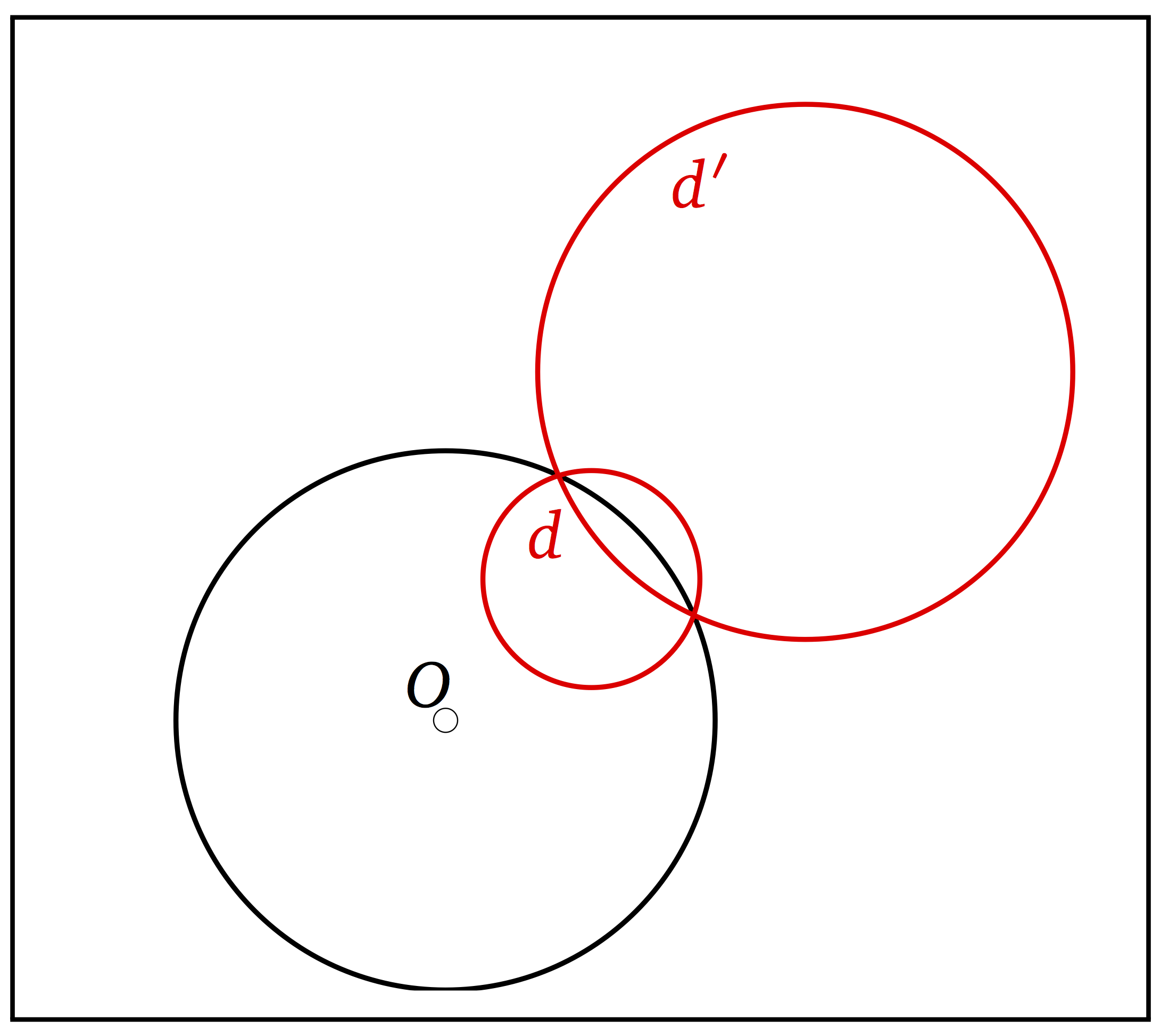
Inverses d’altres circumferències
Si la circumferència passa pel centre i és interior, la seua inversa és una recta exterior. Si la circumferència no passa pel centre, la inversa és una circumferència que és exterior si la primera és interior, i interseca en els mateixos dos punts si interseca amb la circumferència que defineix la inversió.