Mosaics duals
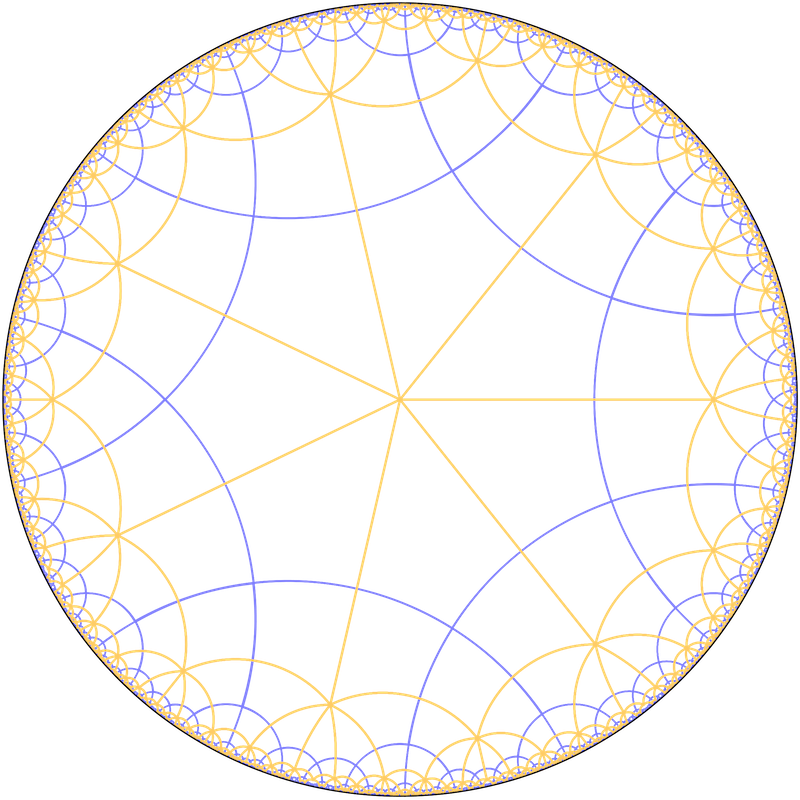
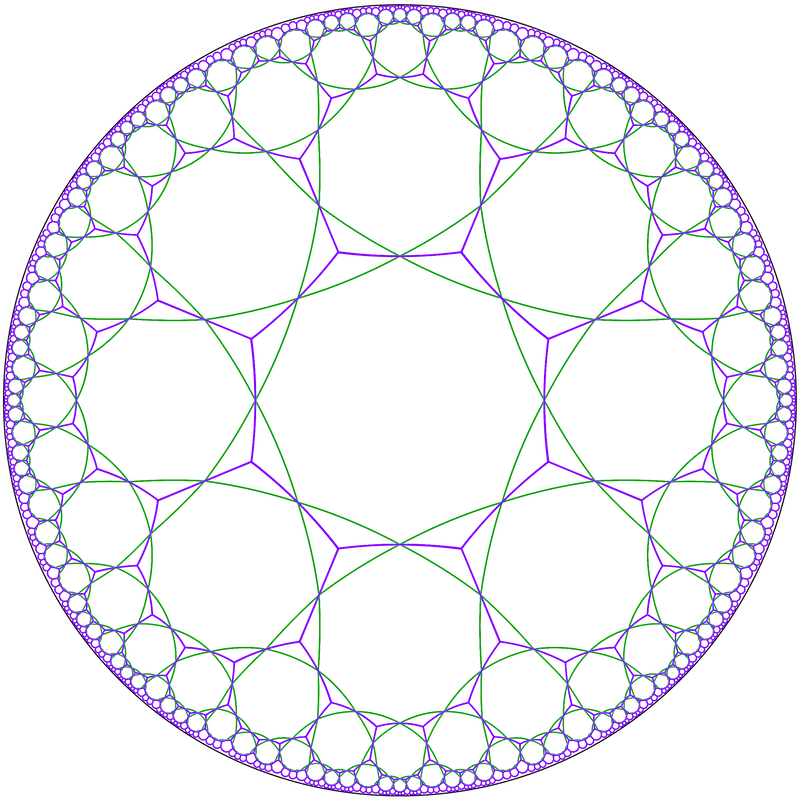
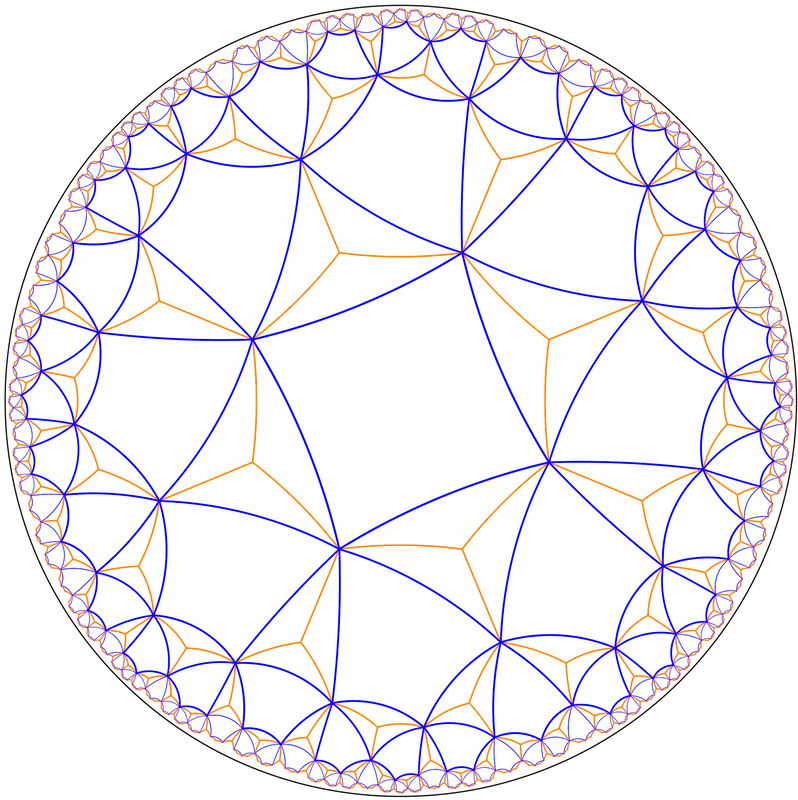
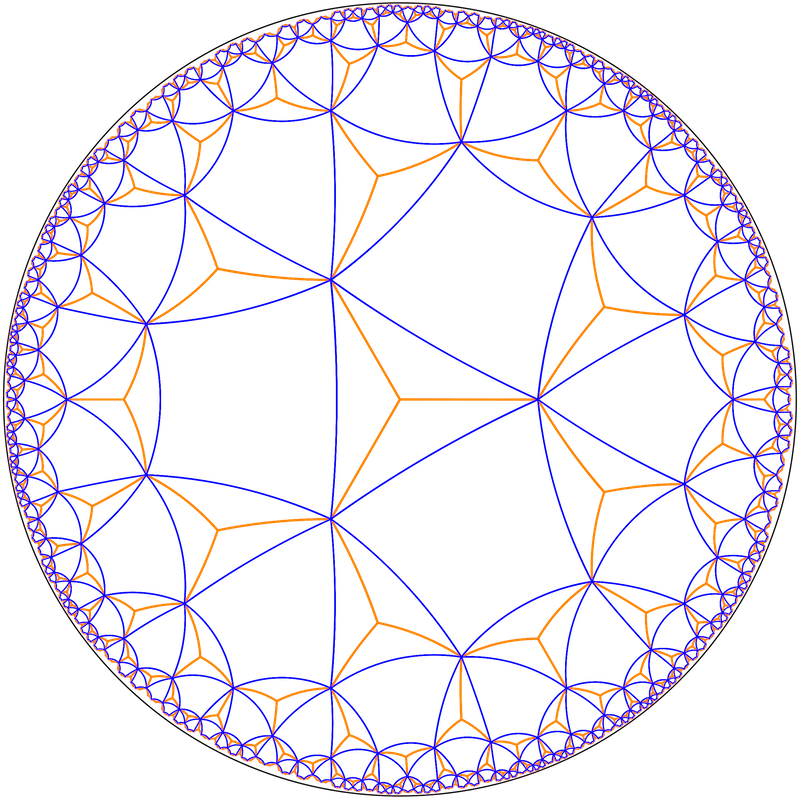
Si en un mosaic hiperbòlic regular unim cada centre d’un polígon amb els centres dels polígons adjacents mitjançant un segment, obtenim un altre mosaic anomenat dual. En particular si ho fem en un mosaic {p,q} amb un polígon centrat en el centre de la circumferència obtenim un altre del tipus {q,p} en què els vèrtexs estan en el centre del disc de Poincaré.
Mosaics en els punts mitjans
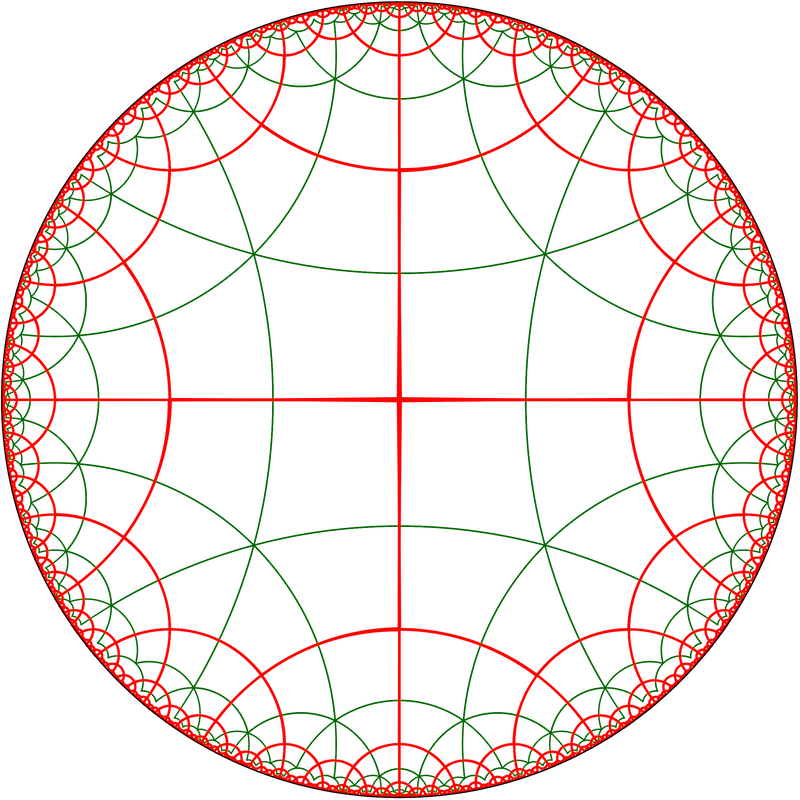
Igual que en els mosaics euclidians es poden crear mosaics unint els punts mitjans dels segments d’un altre mosaic. A partir d’un regular {p,q} apareix un de semiregular p.q.p.q, format per 4 poligons alternant de p i q costats.
Podem assegurar que són semiregulars perquè els costats són iguals en longituds des del punt de vista de la geometria hiperbòlica, ja que tots uneixen punts mitjans de dos costats contigus, i s’uneixen en cada vèrtex els mateixos polígons i en el mateix ordre. En quants als angles dels polígons també hauran de ser iguals perquè tots els segments que uneixen punts mitjans dels polígons estan en posició idèntica.
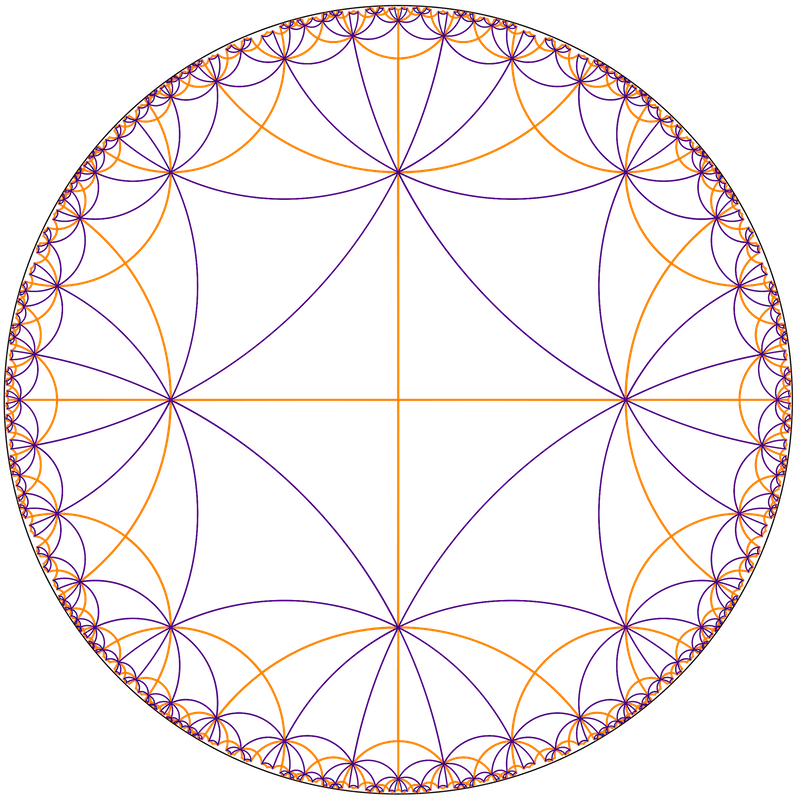
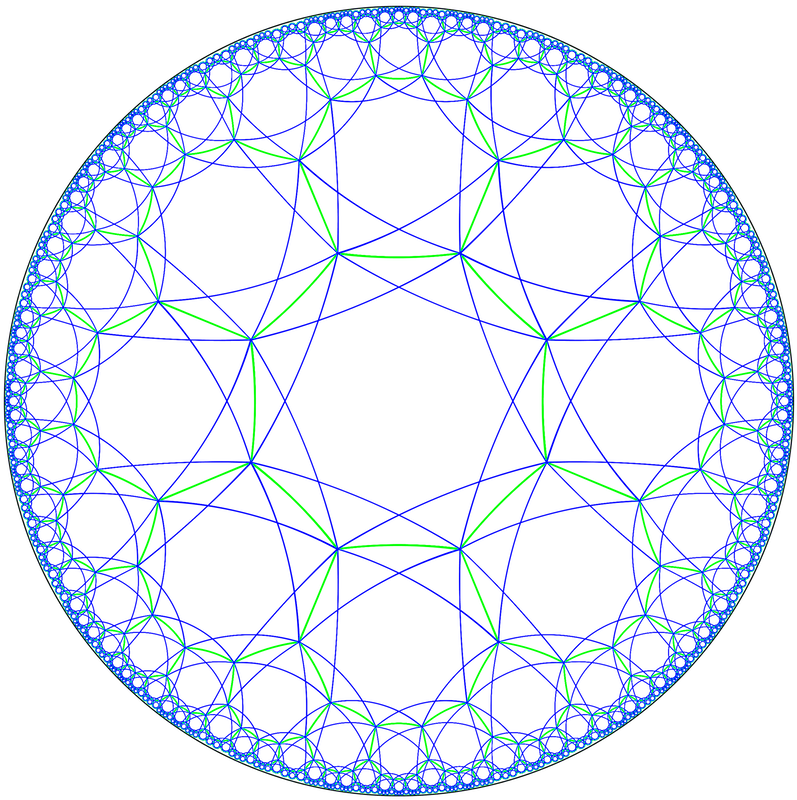
Mosaics amb diagonals
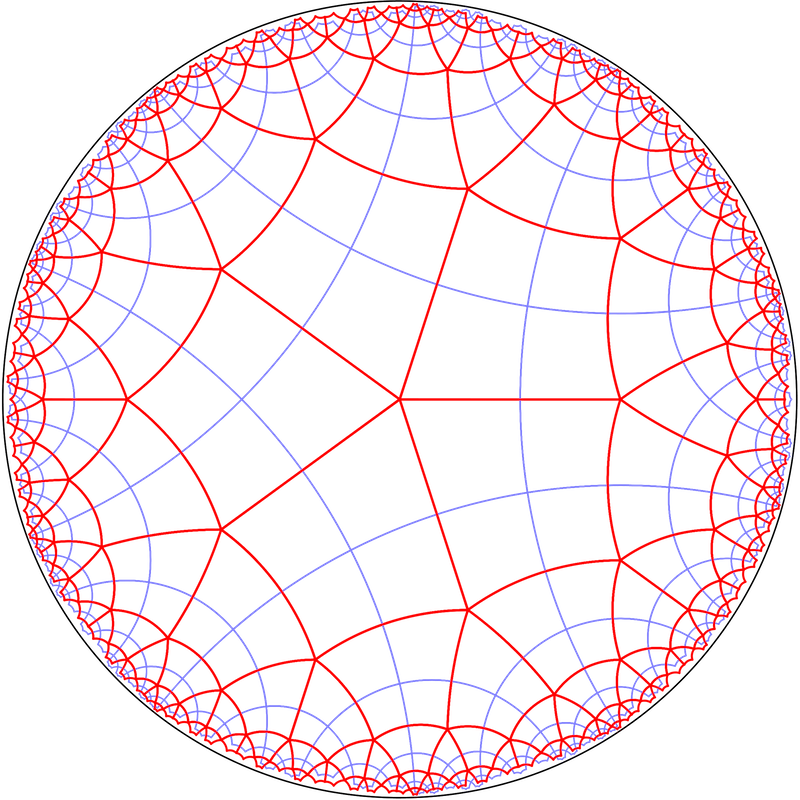
Dibuixant certes diagonals amb segments hiperbòlics podem construir altres mosaics que a vegades tindran una regularitat. Podem construir les diagonals unint vèrtexs alterns, sols la meitat de les possibles diagonals.
Sobre mosaics amb polígon centrat hem construït mosaics 4.3.4.3.4.3 , 4.3.4.3.4.3 i un {6,6} sobre un {8,3}, {6,4} i {4,6} respectivament.
Sobre mosaics amb vèrtex centrat hem construït mosaics 4.3.4.3.4.3 , 4.3.4.3.4.3 i un {6,6} sobre un {8,3}, {6,4} i {4,6} respectivament. Són els mateixos que amb polígon centrat però l’aspecte és totalment diferent.
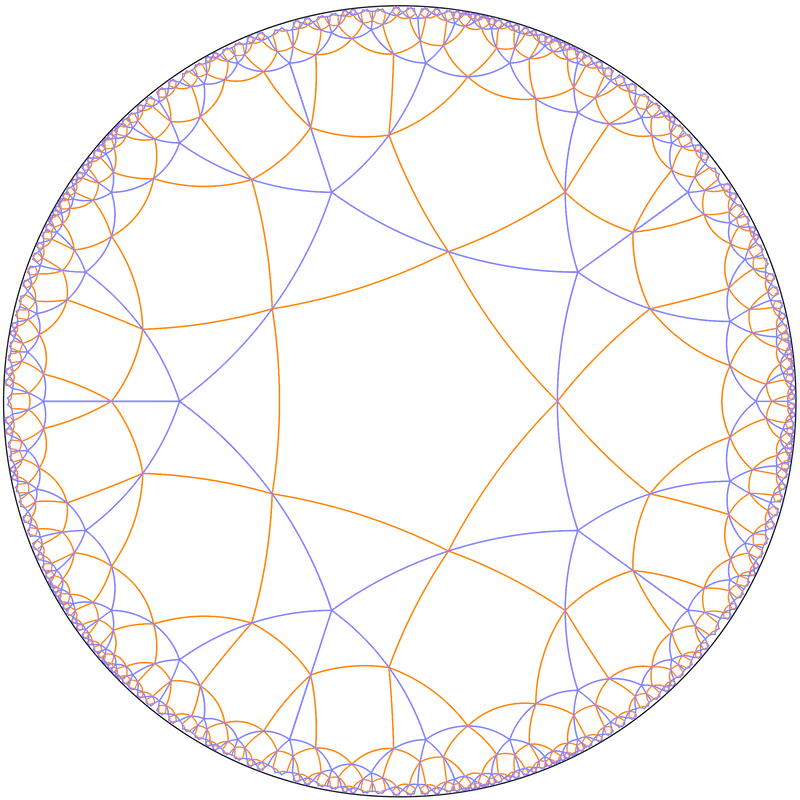
Si dibuixem més diagonals ens trobem amb altres mosaics irregulars. Dos mosaics de rombes sobre un mosaic {4,5} i un {6,5}. I un altre molt irregular sobre un {8,3}