L’angle interior d’un polígon de p costats mesura en radians

En un mosaic amb polígons regulars de p costats i en el que concorren q polígons en un vèrtex la suma de tots els angles al voltant d’un vèrtex serà . Parlarem del mosaic {p,q}

Analitzem en un quadre els valors de  amb valors de p i q entre 2 i 8:

	p=2	3	4	5	6	7	8
q=2	0	0,67	1	1,2	1,33	1,43	1,5
3	0	1	1,5	1,8	2	2,14	2,25
4	0	1,33	2	2,4	2,67	2,86	3
5	0	1,67	2,5	3	3,33	3,57	3,75
6	0	2	3	3,6	4	4,29	4,5
7	0	2,33	3,5	4,2	4,67	5	5,25
8	0	2,67	4	4,8	5,33	5,71	6

Ara observem que quan dóna un valor de 2 (color roig) tenim els únics tres mosaics possibles en el pla euclidià, en un vèrtex poden concórrer 3 hexàgons, 4 quadrats o 6 triangles.

Els valors per a p=2 o q=2 (color gris) són estranys i podem ignorar-los per ara.

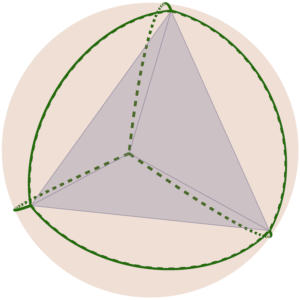
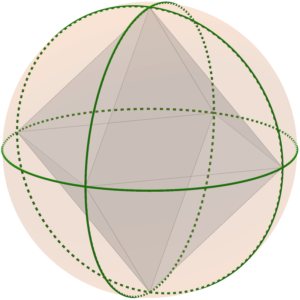
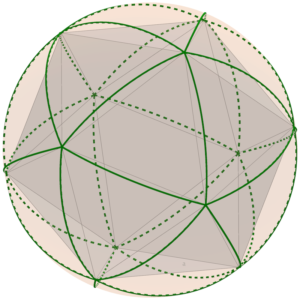
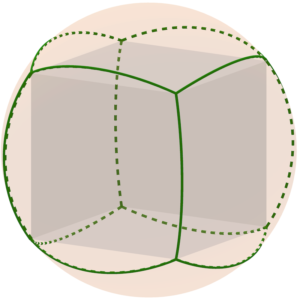
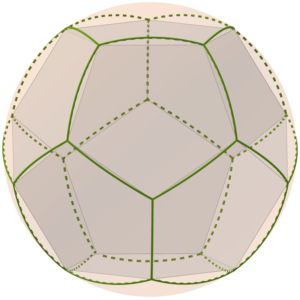
Tenim valors menors de 2 no inclosos en el cas anterior (color blau) i que podem interpretar com mosaics en pla el·líptic com la superfície d’una esfera en la qual és possible que la suma d’angles al voltant d’un punt siga menor que , i que podem interpretar com els 5 poliedres regulars: {3,3} tetraedre, {3,4} octaedre, {3,5} icosaedre, {4,3} cub i {5,3} dodecaedre. En els següents dibuixos podem veure aquests mosaics i unint els vèrtexs els poliedres en l’interior de l’esfera tenim els poliedres inscrits en l’esfera.

La resta de valors majors de 2 seran tots els mosaics regulars en el pla hiperbòlic.